Question

The directed line segment, AB¯, contains the points A(−2,6)

and B(4,−6).
What are the coordinates of the point that partitions AB¯ according to the part-to-part ratio 2:4?

Answer 1

The coordinate of the point is; (0,2)

Explanation:

The given line segment has points with coordinates A(−2,6)

and B(4,−6).

We want to find a point (x,y) that divides this line segment in the ratio:

m:n=2:4

The x-coordinate of this point is given by;

`x=(mx_2+nx_1)/(m+n)`

We substitute
`x_1=-2,x_2=4,m=2,n=4`

`\implies x=(2*4+4*-2)/(2+4)`

`\implies x=(8-8)/(6)=0`

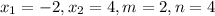
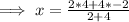
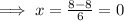
The y-coordinate of this point is given by;

`y=(my_2+ny_1)/(m+n)`

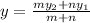
We substitute
`y_1=6,y_2=-6,m=2,n=4`

`\implies y=(2*-6+4*6)/(2+4)`

`\implies y=(-12+24)/(6)=2`

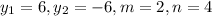
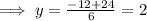
The coordinate of the point is; (0,2)