We have the following differential equation to solve:
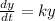
In which we know
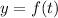
.
First, we'll use "separation of variable" (think of it as treating the differential quantities of a variable as a variable by themselves) to rewrite the differential equation as follows:
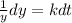
We set an integral in both sides of the equation (keep in mind

is a constant):
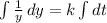
We solve the integral:

In which
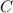
and

are constants, hence we can rewrite the equation with only one constant (lets call it

):
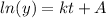
We solve for

:
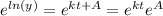
We simplify and notice that
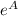
is a constant so can be written with one arbitrary symbol (I'll use
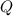
):
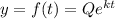
The previous is called the general solution for the differential equation, we're looking for the specific solution given our known values of the function. So now, we need to obtain the values of the constants
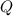
and

, this is done by using the known two values of the function.
Lets start with if
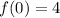
:
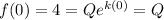
So, we have the value of one constant,
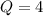
.
Now, lets find the value of the other constant using
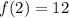
:
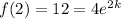
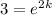

Now that we know both of the constants, we can write the specific solution of the differential equation, which is the answer of the problem:
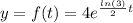 Which is option A.
Which is option A.