Question

What is the second term in the binomial expansion of (2r – 3s)12? –73,728r11s 73,728r11s 608,256r10s2 –608,256r10s2?

Answer 1

It is A, my friend. I have taken the test and got it right ;)

Answer 2

A is the correct option.

Step-by-step explanation:

We have been given that
`(2r - 3s)^(12)`

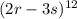
The
`r^(th)` term of a binomial expansion
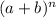`(a+b)^n` is given by

`t_r=^(n)C_(r-1)a^(n-r+1)b^(r-1)`

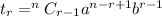
For the given binomial expansion, we have

`a=2r,b=-3s,r=2,n=12`

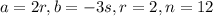
On plugging this value in the above formula, we have

`t_2=^(12)C_(2-1)(2r)^(12-2+1)(-3s)^(2-1)\\\\t_2=^(12)C_1 (2r)^(11)(-3s)^(1)\\\\t_2=(12!)/(1!11!)(2)^(11)r^(11)(-3)s\\\\t_2=12\cdot (2)^(11)(-3)r^(11)s\\\\t_2=-73728r^(11)s`

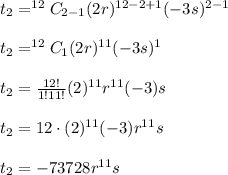
Therefore, the second term is -73728r^11 s

A is the correct option.