Answer:
The coordinates of D are:
(-3,-7)
Explanation:
We know that if a point B(c,d) is located in middle of two points i.e. A(a,b) and C(a',b').
Then the coordinates of B is given by:
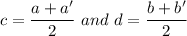
It is given that:
B is the midpoint of AC.
A(-9,-4), C(-1, 6).
Hence, the coordinates of B(x,y) is given by:
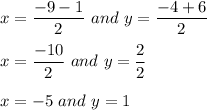
i.e. the coordinates of B are: (-5,1).
E is the midpoint of BD.
Let the coordinates of D be (w,z)
Also, E is located at E(-4,-3).
i.e.
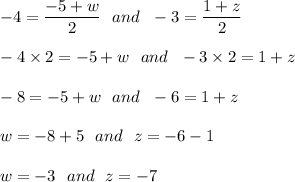
Hence, the coordinates of D are: (-3,-7)