Question

Need help (ignore top part)

Answer 1

The instructions to label the distribution probably are suggesting that you use the empirical (68-95-99.7) rule. It's the one that says approximately 68% of a normal distribution lies within 1 standard deviation of the mean, 95% within 2 standard deviations of the mean, and 99.7% with 3 standard deviations of the mean.

Suppose
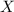
`X` represents the random variable for the number of days a house is on the market. Then what the above means is that for this particular distribution


`\mathbb P(|X-50|\le13)=\mathbb P(37\le X\le63)\approx0.68`


`\mathbb P(|X-50|\le26)=\mathbb P(24\le X\le76)\approx0.95`


`\mathbb P(|X-50|\le39)=\mathbb P(11\le X\le89)\approx0.997`

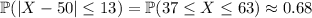
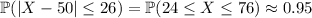
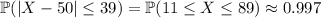
Using these probabilities, and the fact that the distribution is symmetric, you would find

5. 99.7%, following immediately from the rule;

6. 84%. The distribution is symmetric, so exactly 50% falls to either side of the mean. This also means we can split up
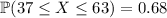
`\mathbb P(37\le X\le 63)=0.68` to find that
`\mathbb P(37\le X\le50)=0.34`;

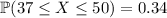
7. 68%, again straight from the rule;

8. 2.5%. About 95% of houses are on the market between 24 and 76 days, so 5% are not. Half of these are on the market for less than 24 days.