Answer:
Option A - If the domain of
 is restricted to
is restricted to
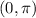 ,
,
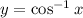 is a function.
is a function.
Explanation:
Given : Expression
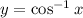
To find : Which statement is correct about the given expression?
Solution :
The domain of the inverse cosine function is [−1,1] and the range is [0,π] .
We have given the inverse function
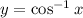
As the domain of
 is restricted to
is restricted to
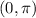 as after
as after
 the value repeats itself and not satisfying the inverse function property.
the value repeats itself and not satisfying the inverse function property.
Therefore, Option A is correct.
If the domain of
 is restricted to
is restricted to
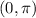 ,
,
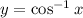 is a function.
is a function.