Question

In triangle ABC, AB = 12 inches, AC = 18 inches and the area of the triangle is 107.737 square inches. What is the measure of angle A?

A) 1.5°
B) 43°
C) 86°
D) 172°

Answer 1

Your answer is c, 86 degrees. Use the sine function, which is depicted in the image below. Hope this helped.

Answer 2

(C)
`86^(\circ)`

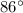
Explanation:

It is given that In triangle ABC, AB = 12 inches, AC = 18 inches and the area of the triangle is 107.737 square inches.

Now, using the formula
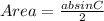`Area=(absinC)/(2)` where a and b are the two sides of the triangle and the C is the included angle, therefore

We have AB=12 in and AC=18 in and area= 107.737 square inches.

Substituting these values in the above equation, we get

`107.737=\frac{12{*}18sinA}{2}`

`107.737=108sinA`

`(107.737)/(108)=sinA`

`0.997=sinA`

`A=sin^(-1)(0.997)`

`A=85.56^(\circ)`

`A`≈
`86^(\circ)`

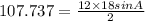
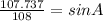
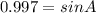
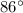
Thus, option (C) is correct.