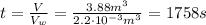Question

A garden hose has a radius of 0.0120 m, and water comes out at a speed of 4.88 m/s. How much time does it take to fill up a kids swimming pool with a volume of 3.88 m^3

Answer 1

Correct Answer:

1758 seconds

Answer 2

The radius of the garden hose is
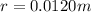
`r=0.0120 m`, so its cross-sectional area is

`A=\pi r^2 = \pi (0.0120 m)^2 = 4.52 \cdot 10^(-4) m^2`

The amount of water (in
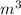
`m^3`) that comes out from the hose in one second is given by the product between the speed of the water and the cross-sectional area of the hose:

`V_w = A v = (4.52 \cdot 10^(-4)m^2)(4.88 m/s)=2.2 \cdot 10^(-3) m^3/s`

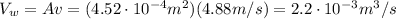
The time needed to fill the pool is equal to the volume of the pool divided by the amount of water that comes out every second:

`t= (V)/(V_w)= (3.88 m^3)/(2.2 \cdot 10^(-3)m^3)=1758 s`