Question

Which of the following points could be the initial point of vector v if it has a magnitude of 10 and the terminal point (-2,4)?

a. (-0.2, 0.4)
b. (-8, -4)
c. (-12, -6)
d. (1, 3)

Answer 1

Use the distance formula;
10=√(-2-x)²+(4-y)²
Now put the options one by one into the above equation;
you find that option b satisfies the equation which is the correct answer.

Answer 2

The initial point is (-8, -4)

Explanation:

Given that the terminal point is (-2,4) and the magnitude of vector v is 10 then we have to find the initial point.

Let the initial point is (x, y).

`\text{By distance formula, the length of line joining the points }(x_1,y_1)\text{ and }(x_2, y_2)`

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

`10=√((-2-x)^2+(4-y)^2)`

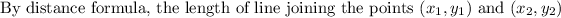
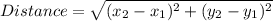
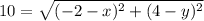
The point which satisfy the above condition is the initial point

Option a: (-0.2, 0.4)

`10=√((-2-(-0.2))^2+(4-0.4)^2)=√(3.24+12.96)=√(16.2)=4.02`

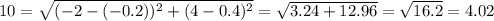
Not satisfied

Option b: (-8, -4)

`10=√((-2-(-8))^2+(4-(-4))^2)=√(36+64)=√(100)=10`

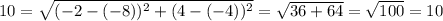
Satisfied

Option c: (-12, -6)

`10=√((-2-(-12))^2+(4-(-6))^2)=√(100+100)=√(200)=14.1`

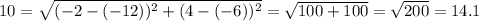
Not satisfied

Option d: (1, 3)

`10=√((-2-1)^2+(4-3)^2)=√(9+1)=√(10)=3.2`

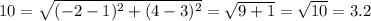
Not satisfied

Hence, option 2 is correct.

The initial point is (-8, -4)