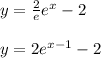Question

Consider the following properties of the graph of an exponential function.

a. Horizontal Asymptote at x=-2
b. The graph is increasing from (-infinity, infinity)
c. The x-intercept is at (1,0)
What is the equation for this graph?

Answer 1

The parent exponential function is:


`y= e^(x)`

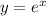
The Horizontal asymptote of parent exponential function is y =0. For the function to have asymptote y=-2, it must be shifted 2 units down. So resulting graph will be:


`y=e^(x) -2`

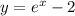
The function is increasing from left to right.

The above function does not have x-intercept at (1,0). For the function to have an x-intercept at (1,) it must be multiplied with some co-efficient as shown below:


`y=a e^(x)-2`

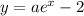
For x=1, y=0. So we can write:


`0=a e^(1)-2 \\ \\ 2=ae \\ \\ a= (2)/(e)`

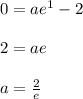
So, the exponential function satisfying the given conditions will be:


`y= (2)/(e) e^(x)-2 \\ \\ y=2 e^(x-1) -2`