Question

Can someone please help with this trig question?

Answer 1

First we must understand how to write a logarithmic function:


`log_(b)a=x`

In the equation above, b is the base, x is the exponent, and a is the answer. These same variables can be rearranged to be expressed as an exponential equation as followed:


`b^x=a`

Next, we need to understand basic logarithm rules.

1. When a value is raised to a power, we can move the exponent to the front of the logarithm. Example:

log(a^2) = 2log(a)

2. When two variables are multiplied together, we can add the logarithms of the individual variables together. Example:

log(ab) = log(a) + log(b)

3. When a variable is divided by another variable, we can subtract the logarithms of the individual variables. Example:

log(a/b) = log(a) - log(b)

Now we can use these rules to solve the problem.


`log(r)=log( \sqrt[3]{ (A^2B)/(C) } )`

We can rewrite the cube root as:


`log(r) = log( ((A^2B)/(C))^ (1)/(3) )`

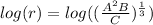
Now we can move the one-third to the front:


`log(r) = (1)/(3) log( (A^2B)/(C) )`

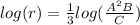
Now we can split up the logarithm:


`log(r) = (1)/(3) (log(A^2)+log(B)-log(C))`

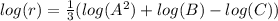
Finally, we can move the exponent to the front of the log of A:


`log(r) = (1)/(3) (2log(A)+log(B)-log(C))`

Distribute the one-third to get the answer:


`log(r) = (2)/(3) log(A) + (1)/(3) log(B) - (1)/(3) log(C)`

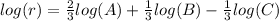The answer is (4).