Question

What system of inequalities is represented by the graph?

A. y < or equal to 5x -1 and -3x + y > or equal to 4
B. y < or equal to 5x -1 and 3x + y > or equal to 4
C. y < or equal to 5x + 1 and 3x + y > or equal to 4
D. y < or equal to 5x - 1 and 3x + y > or equal to -4

Answer 1

As shown in the figure, we have two straight line. One of them has a negative slope and the other has a positive one. In two dimensions, the equation for non-vertical lines is often given in the slope-intercept form by:


`y=mx+b`

being m the slope of the line and b the y-intercept of it.

On the other hand, if x = 0 then y = b.

First of all we will order the equations above without inequalities like this:

A.
`y = 5x-1`,
`y = 3x+4`
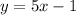B.
`y = 5x-1`,
`y = -3x+4`
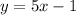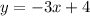
C.
`y = 5x+1`,
`y = -3x+4`
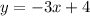
D.
`y = 5x-1`,
`y = -3x-4`

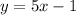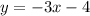
As shown in the figure b = -1 for one straight and b = 4 for the second one. This values take place when x = 0. So, we discard C and D, because if x = 0, then:

For C, b = 1 and b = 4
For D, b = -1 and b = -4

Let's analyze A and B. So:

For A, m = 5 and m = 3
For B, m = 5 and m = -3

Therefore, we discard A because of the statement above.

Finally the answer is B. So, the inequalities are:

(1)
`y\ \textless \ 5x-1`
(2)
`3x+y \geq 4`

Let's prove this answer. We will take the point (2, 0) that is in the region in gray. So, substituting this point in the inequalities, we have:

(1)
`0\ \textless \ 9`
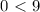
(2)
`6 \geq 4`

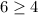
In fact, this is true.