Question 1:
Consider the equation
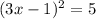
Taking square root on both the sides of the equation, we get

Consider
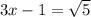
adding '1' to both sides, we get
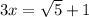
Dividing by '3', we get
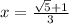
Consider
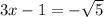
adding '1' to both sides, we get
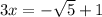
Dividing by '3', we get
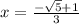
So, the solution set for this equation is
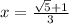 and
and
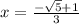 .
.
Question 2:
Consider the equation
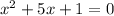
We will use quadratic formula, we get
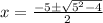
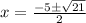
So, the solution set for this equation is
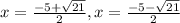 .
.
Question 3:
Consider the equation
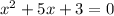
By using the quadratic formula, we get
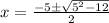
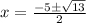
so, the solution set for this equation is
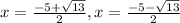 .
.