Question

Type the correct answers out, thank you - 20 POINTS

Answer 1

AB and BC form a right angle at their point of intersection. This means AB is perpendicular to BC.

We are given the coordinates of points A and B, using which we can find the equation of the line for AB.

Slope of AB will be:


`m= (-1-1)/(14-2)=-1/6`

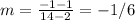
Using this slope and the point (2,1) we can write the equation for AB as:


`y-1= (-1)/(6)(x-2) \\ \\ y= -(1)/(6)x+ (1)/(3)+1 \\ \\ y=-(1)/(6)x+ (4)/(3)`

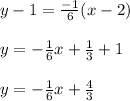
The above equation is in slope intercept form. Thus the y-intercept of AB is 4/3.

Slope of AB is -1/6, so slope of BC would be 6. Using the slope 6 and coordinates of the point B, we can write the equation of BC as:

y - 1 = 6(x - 2)
y = 6x - 12 + 1
y = 6x - 11

Point C lies on the line y = 6x - 11. So if the y-coordinate of C is 13, we can write:

13 = 6x - 11
24 = 6x
x = 4

The x-coordinate of point C will be 4.

Therefore, the answers in correct order are:

4/3 , 6, -11, 4