Question

Find the length of AB , given that DB is a median of the triangle and AC = 24.

Answer 1

AB=12 because medians bisect the opposing side of a vertex.

Answer 2

AB = 12 units

Explanation:

We are given the following information in the question:

DB is the median of the triangle.

AC = 24 units

Property of median of a triangle:

• A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side.

• Thus, a median divides the side of triangle in two equal parts.

Thus, DB divides AC in two equal parts.

Thus, we could say:

AB = BC

We have to find the length of AB.

`\text{AB} = \displaystyle(AC)/(2) = (24)/(2) = 12\text{ units}`

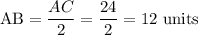
Thus, AB is 12 units.