We have the sample size, sample mean and the sample standard deviation. Since the population standard deviation is not know, we will use t-distribution to find the confidence interval.
The critical t value for 95% confidence interval and 63 degrees of freedom is 1.998.
The 95% confidence for the population mean will be:
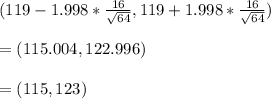
Thus, the 95% confidence interval for the population mean will be (115,123)
So, option A is the correct answer