Question

Which statement best describes the graph of −x3 − x2 + 4x + 4?

Answer 1

for
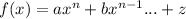
`f(x)=ax^n+bx^(n-1)...+z` where n is the highest power of the function
if n is even and 'a' is positive, the graph goes from top left to top right
if n is even and 'a' is negative, the graph goes from bottom left to bottom right
if n is odd and 'a' is positive, the graph goes from bottom left to top right
if n is odd and 'a' is negative, the graph goes from top left to bottom right


and, for
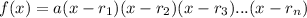
`f(x)=a(x-r_1)(x-r_2)(x-r_3)...(x-r_n)`, it intersects the graph at
`x=r_1`,
`x=r_2`,
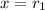
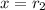
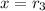
`x=r_3`, up to
`x=r_n`,

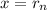
so see what we've got
`f(x)=-x^3-x^2+4x+4`
factor and group

`-x^3-x^2+4x+4=(-x^3-x^2)+(4x+4)=`
`(-x^2)(x+1)+(4)(x+1)=(x+1)(4-x^2)=(x+1)(2-x)(2+x)=`
`-1(x+2)(x+1)(x-2)`
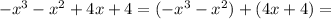
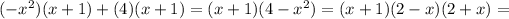
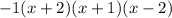
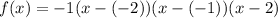
`f(x)=-1(x-(-2))(x-(-1))(x-2)` a=-1 the roots are x=-2, x=-1, x=2 since n=3 (from
`-x^3-x^2+4x+4`) and a is negative, we know it goes from top left to bottom right also, it intersects at x=-2,-1, and 2

answer is the 3rd option: It starts up on the left and goes down on the right and intersects the x-axis at x = −2, −1, and 2.