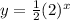Answer:
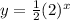
Explanation:
The given equation is
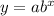
It passes through the points (4, 8) and (6, 32). Hence, we have

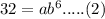
Divide equation (2) by (1)
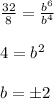
For b = 2
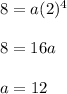
For b = -2
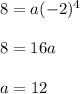
Thus, the values of a and b are
a= 1/2, b = 2 and a= 1/2, b=-2
Thus, the exponential equation is