Question

What are the zeros of the quadratic function f(x) = 6x2 + 12x – 7?

Answer 1

Thus, the zeros are x=0.47,-2.47

Step-by-step explanation:

We have been given the function

`f(x)=6x^2+12x-7`

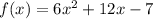
In order to find the zeros of this function, we will solve the quadratic equation
`f(x)=6x^2+12x-7=0`

We'll solve this by quadratic formula which is given by

`x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

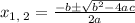
We have

`a=6,\:b=12,\:c=-7:`

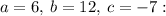
On substituting these values, we get

`x_(1,\:2)=(-12\pm √(12^2-4\cdot \:6\left(-7\right)))/(2\cdot \:6)\\\\x_(1,\:2)=(-12\pm √(312))/(2\cdot \:6)\\x_(1,\:2)=(-12\pm 2√(78))/(12)\\\\\mathrm{The\:final\:solutions\:to\:the\:quadratic\:equation\:are:}\\\\x=(√(78)-6)/(6),\:x=-(6+√(78))/(6)\\\text{In decimal, we have}\\x=0.47,-2.47`

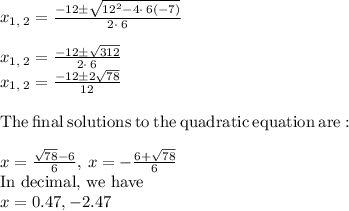
Thus, the zeros are x=0.47,-2.47

Answer 2

Given the equation:


`f(x)=6x^(2)+12x-7`

The question is: What are the zeros of this quadratic function? this happens when f(x) = 0, so:


`f(x)=6x^(2)+12x-7=0`

a = 6
b = 12
c = -7

Then the zeros are given through equation:


`x_(12)= \frac{-b\pm \sqrt{b^(2)-4ac}}{2a}= \frac{-12\pm \sqrt{12^(2)-4(6)(-7)}}{2(6)}`

∴
`x_(1)=0.47`

`x_(2)=-2.47`