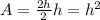Question

What is the area of an isosceles trapezoid if the length of an altitude is h, and diagonals are perpendicular to each other?

Answer 1

In order to answer that question, you have to work with right triangles in this ABCD trapezoid. Because of diagonals are perpendicular, we say that ΔAOD and ΔBOC are right-isosceles triangles. ∠OBC= ∠FBD = 45°. Then, BF = FD = h. Similarly, in triangle ACE ∠ACE = 45°. From here, CE = AE = h.

The area of this trapezoid is
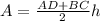
`A= (AD+BC)/(2)h`. We need to find AD and BC in order to calculate this area. Since we know that BC = FE. AE + FD = AD + BC. We know that AE + FD = 2h.

The area is
`A= (2h)/(2) h = h^(2)`