Question

Which angle of rotation is determined by the matrix below? (pictured above)

A. 45 degrees

B. 135 degrees

C. 225 degrees

D. 315 degrees

Answer 1

I think the answer is C hope this would help you

Answer 2

Option C. 225 degrees

Explanation:

The given matrix is

`\begin{bmatrix}-(√(2))/(2) & (√(2))/(2)\\ -(√(2))/(2) & -(√(2))/(2)\end{bmatrix}`

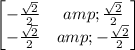
which is in the form of

`\begin{bmatrix}cos\phi & -sin\phi \\ cos\phi & sin\phi \end{bmatrix}`

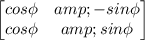
where ∅ is the angle of rotation of any vector.

By comparing the elements of first column of two matrices given

Value of cos ∅ = -√2/2

∅ = either 225° or 315°

and it is also given that (sin ∅) = -√2/2 or sin ∅ = -√2/2

Therefore ∅ = either 225° or 315°

Now sin ∅ = -√2/2

∅ = either 135° or 225°

So the common angle is 225°

Now it's confirmed that measurement of angle ∅ = 225°

Option C. 225° degrees is the answer.