Question

What is the average rate of change of f(x), represented by the table of values, over the interval [-3, 2]?

x f(x)
-5 -150
-3 -36
-1 -2
0 0
1 0
2 4
-40
-8
8
32

Answer 1

You would select the points with the x-values -3 and 2 and use the slope formula:
(-3, -36) and (2,4)

`m= (y_2-y_1)/(x_2-x_1)` ← slope formula
x1 = -3 y1 = -36 and x2 = 2 y2 = 4


`m= (4--36)/(2--3) = (40)/(5) =8`

Answer 2

Option C

Explanation:

The average rate of change of f(x) will be represented by the slope between the given interval [-3, 2]

For x = -3 value of f(x) = -36

and for x = 2 value of f(x) = 4

So there are two points ( -3, -36 ) and ( 2, 4 ) through which function is defined.

Therefore, from the formula of slope =
`(y-y')/(x-x')`

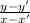
slope =
`(4+36)/(2+3)`

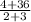
= slope =
`(40)/(5)`

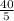
= 8

Option C is the answer.