Answer:
12.9 centimeters
Explanation:
The given equation is
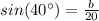
Where
 represents the length of the segment AC, according to the given graph.
represents the length of the segment AC, according to the given graph.
To find
 we just need to isolate it in the given equation,
we just need to isolate it in the given equation,
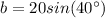
Then, we know that
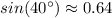 , so
, so
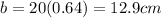
Therefore, the length of segment AC is 12.9 centimeters, rounded to the nearest tenth.