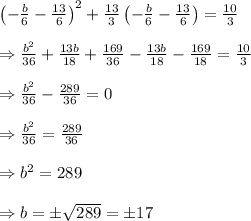Question

The difference between the roots of the equation 3x2+bx+10=0 is equal to 4 1 3 . find
b.

Answer 1

The answer is 17 and -17

Explanation:

Answer 2

Given that the difference between the roots of the equation
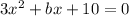
`3x^2+bx+10=0` is
`4 (1)/(3) = (13)/(3)`.

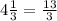
Recall that the sum of roots of a quadratic equation is given by
`- (b)/(a)`.

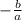
Let the two roots of the equation be
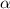
`\alpha` and
`\alpha + (13)/(3)`, then


`\alpha + \alpha + (13)/(3) =2 \alpha + (13)/(3) =- (b)/(a) =- (b)/(3) \\ \\ i.e.\ \ 2 \alpha + (13)/(3)=- (b)/(3)` . . . (1)

Also recall that the product of the two roots of a quadratic equation is given by
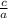
`(c)/(a)`, thus:


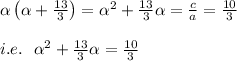
`\alpha \left( \alpha + (13)/(3) \right)= \alpha ^2+ (13)/(3) \alpha = (c)/(a) = (10)/(3) \\ \\ i.e.\ \ \alpha ^2+ (13)/(3) \alpha=(10)/(3)` . . . (2)

From (1), we have:


`2 \alpha =- (b)/(3) - (13)/(3) \\ \\ \Rightarrow \alpha =- (b)/(6) - (13)/(6)`

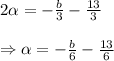
Substituting for alpha into (2), gives:


`\left(- (b)/(6) - (13)/(6)\right)^2+ (13)/(3) \left(- (b)/(6) - (13)/(6)\right)= (10)/(3) \\ \\ \Rightarrow (b^2)/(36) + (13b)/(18) + (169)/(36) - (13b)/(18) - (169)/(18) = (10)/(3) \\ \\ \Rightarrow (b^2)/(36) - (289)/(36) =0 \\ \\ \Rightarrow (b^2)/(36) = (289)/(36) \\ \\ \Rightarrow b^2=289 \\ \\ \Rightarrow b=\pm√(289)=\pm17`