First we are going to find the slope of these two endpoints.
Slope =

Slope =
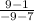
Slope =
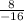
Slope =
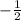
Because we need the perpendicular bisector, we do the opposite reciprocal of the slope. This is positive two.
Your perpendicular equation begins as y = 2x + b
To find where it will bisect, we need to find the midpoint of the two endpoints.
Midpoint =
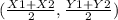
Mdpt =
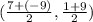
Mdpt =

Mdpt = (- 1, 5)
We plug this into our incomplete equation to solve for b.
5 = 2(- 1) + b
5 = - 2 + b
7 = b
Your perpendicular bisector equation is y = 2x + 7