Question

The sum of two integers is 26. the sum of the squares of the two integers is 340. what is the product of the two numbers?

Answer 1

Lets say that the two unknown integers are
`n` and
`m`.

We know the following things about
`n` and
`m`:


`n+m=26`

`n^2+m^2=340`

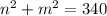
And, we want to find
`nm`.

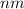
To solve this, we'll use the expansion of the squared of the sum of any two inegers; this is expressed as:


`(n+m)^2=n^2+2nm+m^2`

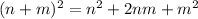
So, given what we know about the unknown integers, the previous can be written as:


`(26)^2=340+2nm`

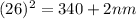
We can easily solve for
`nm`:


`nm= ((26)^2-340)/(2)= (676-340)/(2)= (336)/(2)=168`

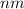
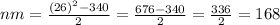The answer is 168.

Another approach to solve the problem is, from the two starting equations, compute the values of
`n` and
`m`, which are 12 and 14, and directly compute their product; however, the approach described is more elegant.