Question

Can derivatives be used to measure the the slope of the tangent line at x=a

Answer 1

Yes. In fact, that is basically the definition of a derivative. It is the instantaneous rate of change of a function.

For example, picture the graph of the following function:


`f(x) = x^2`

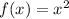
The slope is constantly changing at every x-value, so to find the slope at x=a, we find the derivative of the function.


`f'(x)=2x`

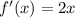
Once we have the derivative, simply plug in a for x to find the slope of the line tangent to f(x) at x=a.

For example, at x=5:


`f'(5)=2(5)`

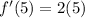
The slope of f(x) at x=5 is 10.