Question

A prior study estimated as 34%. The analysts would like to conduct a second study on the same topic with a margin of error, E, of 0.027 and a confidence level of 90% (z*-score 1.645). What is the minimum sample size that should be used so the estimate of will be within the required margin of error of the population proportion? n = (1 – ) • 17 23 430 833

Answer 1

Answer: 833

Explanation:

When the prior population proportion (p) is known , then the formula to find the minimum sample size is given by :-

`n=p(1-p)((z_(c))/(E))^2`

where,
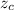`z_(c)` is the z-score for confidence level (c) and E = the margin of error .

Given : A prior study estimated as 34%.

i.e. p= 0.34

Confidence level = 0.90

Critical z-score for 90% confidence level :
`z_(c)1.645`

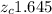
Margin of error : E= 0.027

then , the sample size =
`n=0.34(1-0.34)((1.645)/(0.027))^2`

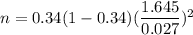
Simplify ,

`n=832.9657\approx833`

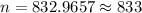
Hence, the minimum sample size=833

Answer 2

The minimum sample size required for a test with a confidence interval of
`100(1 - \alpha )%` with a z-score of
`z_( \alpha /2)` and margin of error of E and a population proportion of p is given by:


`n= (p(1-p)z_( \alpha /2)^2 \alpha )/(E^2)`

Given p = 34% = 0.34, E = 0.027,
`z_( \alpha /2)=1.645`

Therefore,


`n= (0.34(1-0.34)(1.645)^2)/(0.027^2) \\ \\ = (0.34(0.66)(2.706025))/(0.000729) = (0.60723201)/(0.000729) \\ \\ =832.97=833`