Answer:
 square units.
square units.
Explanation:
We draw a ABCD isosceles trapezoid (see in the figure ), in which the length of leg is 26 cm (side AD and side BC), diagonals perpendicular to each other and an altitude (line segment DE or CF ) from the vertex of an obtuse angle to the base divides the longer base into two parts, such that the shorter part is 10 cm long.
Now in triangle ADE (see in figure ), AD =26 cm, AE =10 cm and ∠DEA =90 degree.We apply the Pythagoras theorem in triangle ADE ,then we write
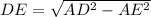 units
units
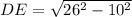 units
units
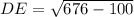 units
units
 units
units
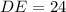 units.
units.
If we see in triangle DOC the side DO and Side CO are same and angle DOC =90 degree, because the given trapezium is an isosceles trapezium and diagonals of trapezium are perpendicular to each other,then triangle DOC is an isosceles right triangle.
Again if we see in triangle DEB angle DEB =90 degree, ∠EDB and ∠EBD are same because ∠DEB =90 degree and ∠ABD =∠CDB =45 degree (see in figure), so triangle DEB is isosceles right triangle and we say that line segment DE =line segment EB. But the line segment DE =24 units ( from above calculation ), so line segment BE = 24 units.
We write from figure,
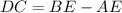 units
units
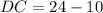 units
units
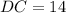 units and
units and
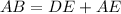
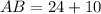 units
units
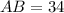 units.
units.
Hence area of isosceles trapezoid =
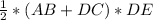 square units
square units
or area of isosceles trapezoid =
 square units
square units
or area of isosceles trapezoid =
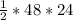 square units
square units
or area of isosceles trapezoid =
 units
units
or area of isosceles trapezoid =
 square units.
square units.