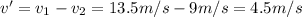Question

A cyclist is going in the positive x-direction at 9m/s. A car initially at rest, accelerates for the first 10 seconds, then it goes with a constant velocity. If the car reaches the cyclist after 15 seconds from the moment the car started moving, find: (a) The acceleration of the car during the first 10 seconds, (b) The velocity of the cyclist with respect to the car when the car reaches the cyclist

Answer 1

1) The car is initially at rest, and it accelerates for the first 10 seconds with acceleration a, so the distance it covers in these first 10 seconds is (in meters)

`d_1 = (1)/(2)at^2 = (1)/(2)a(10 s)^2 = 50 a`
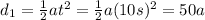
The velocity the car has reached after these 10 seconds is

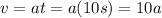
`v=at = a (10 s)=10 a` (3)
Then the car moves for other 5 seconds with this constant velocity (v=10 a) before reaching the cyclist. During this time, the distance it covers is

`d_2 = v t = 10 a \cdot (5 s) =50 a`
So the total distance covered by the car is

`d=d_1 + d_2 = 50 a + 50 a =100 a` (1)

The cyclist is moving at constant speed of
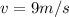
`v=9m/s`, so the distance it covered during the 15 seconds is

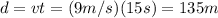
`d=vt=(9m/s)(15 s)=135 m` (2)

And since the car covered the same distance during this time, we can use (1) and (2) to find the acceleration of the car during the first 10 seconds:

`a= (d)/(100)= (135)/(100) = 1.35 m/s^2`


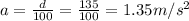
2) The velocity of the car when it reaches the cyclist is given by (3):

`v_1= 10 a= (10 s)(1.35 m/s^2) = 13.5 m/s`
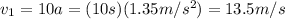
The velocity of the cyclist is
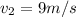
`v_2 = 9m/s`, therefore the velocity of the car relative to the cyclist is

`v' = v_1 - v_2 = 13.5 m/s - 9m/s=4.5 m/s`