The zeroes of a polynomial are the numbers that can be substituted in for x to get a solution of f(x) = 0. To find the zeroes of a polynomial, you would want to factor it and set the factored form equal to zero.
1) First factor the polynomial. The factored form of
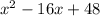
is (x + a)(x + b), where a and b are two numbers that multiply to 48 and add up to -16.
By plugging in and testing numbers that are factors of 48, you can find that 12 x 4 = 48, but also remember that you want those factors to add up to -16. Remember that two negatives multiplied make a positive, so -12 x -4 is also equal to 48! You values for a and b are then -12 and -4!
2) Putting your polynomial into factored form and setting it equal to zero, you get: (x - 12)(x - 4) = 0
Now you want to find values of x where the function is equal to 0. Remember that anything multiplied by 0 is equal to zero. That means you can set each factor equal to 0 to find the two values of x (aka the zeroes)!
Factor 1:
x - 12 = 0
x = 12
Factor 2:
x - 4 = 0
x = 4
Your two zeroes are 12 and 4.
--------
Answer: 12 and 4