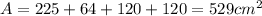Question

Find the area of an isosceles trapezoid, if the lengths of its bases are 16 cm, and 30 cm, and the diagonals are perpendicular to each other.

Answer 1

`A=225+64+120+120=529cm^2`

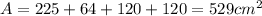
Explanation:

Let A, B, C and D are the vertices of the trapezoid, so that the trapezoid is ABCD.

Let AB be the longer base of 30 cm and CD be the shorter base of 16 cm.

Let the point O be the intersection of diagonals, Then the triangles AOB, BOC, COD and AOD are right angled triangles.

Now, from ΔAOD and ΔBOC, we have

∠AOD=∠BOC=90°

AD=BC (sides of trapezium)

thus, by RHS rule ΔAOD≅ΔBOC

similarly, ΔDOC≅ΔAOB.

Since the trapezoid ABCD has equal lateral sides, the triangle AOB is isosceles right angled triangle.

And since it base AB is 30 cm, its sides (the legs) AO and BO are
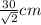`(30)/(√(2))cm`long in measure.

Similarly, the triangle COD is isosceles right angled triangle. and since the base CD is 16 cm, its sides (the legs) CO and DO are
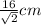`(16)/(√(2))cm`long in measure.

Now, areas of triangles are:

For triangle AOB, the area is:

`A=(1)/(2)((30)/(√(2)))((30)/(√(2)))=225cm^2`

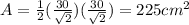
For triangle COD, the area is:

`A=(1)/(2)((16)/(√(2)))((16)/(√(2)))=64cm^2`

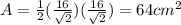
For triangle BOC, the area is:

`A=(1)/(2)((30)/(√(2)))((16)/(√(2)))=120cm^2`

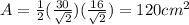
For triangle AOD, the area is:

`A=(1)/(2)((30)/(√(2)))((16)/(√(2)))=120cm^2`

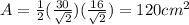
since, total area of the trapezoid is the sum of areas of triangles, therefore we have

`A=225+64+120+120=529cm^2`