Question

PLEEEEEAAAASSSSEEEE!!!!! MULTIPLE CHOICE!!! HELP!!!

1.) Four beats per second are heard when an unknown tuning fork and a 240 Hz tuning fork are struck simultaneously. Select the TWO possible frequencies of the tuning fork.
240 Hz
236 Hz
244 Hz
238 Hz

2.) Four beats per second are heard when an unknown tuning fork and a 240 Hz tuning fork are struck simultaneously. This same unknown tuning fork and a 250 Hz tuning fork are struck. Six beats are heard. Its exact frequency:
is 256 Hz
is 236 Hz
is 244 Hz
cannot be determined

Answer 1

1) The beat frequency related to the interference between two waves is given by

`f_b = |f_1 - f_2|`
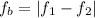
where
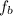
`f_b` is the beat frequency, and
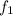
`f_1` and
`f_2` are the frequencies of the two waves.

In our problem ,the beat frequency is
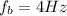
`f_b = 4 Hz`, and one of the two frequencies is
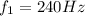
`f_1=240 Hz`, so the frequency of the unknown tuning fork can be:

`f_2 = f_b + f_1 = 4 Hz + 240 Hz = 244 Hz`

`f_2 = f_1 - f_b = 240 Hz - 4 Hz = 236 Hz`

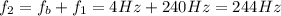
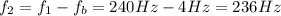
2) Given the previous problem, the frequency of the unknown tuning fork can be either 236 Hz or 244 Hz. When this unknown fork is struck with another fork of 250 Hz, the beat frequency is 6 Hz. Therefore, the only possibility is that the frequency of the first tuning fork is 244 Hz; in fact, we have:

`f_b = |f_1 - f_2|=|244 Hz - 250 Hz|= 6 Hz`