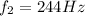Question

Four beats per second are heard when an unknown tuning fork and a 240 Hz tuning fork are struck simultaneously. This same unknown tuning fork and a 250 Hz tuning fork are struck. Six beats are heard. Its exact frequency: is

256 Hz is
236 Hz is
244 Hz
cannot be determined

Answer 1

When the tuning forks are struck simultaneously, the beat frequency is equal to the absolute value of the difference between the frequencies of the two tuning forks:

`f_b = |f_1 - f_2|`
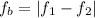
where
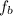
`f_b` is the beat frequency, and
`f_1, f_2` are the frequencies of the two forks.

In the first part of the problem,
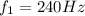
`f_1 = 240 Hz` and
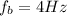
`f_b=4 Hz`, with
`f_2` being the frequency of the unknown fork. In the second part of the problem,
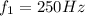
`f_1=250 Hz` and
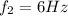
`f_2 = 6 Hz`. So we have the following system of two equations:

`4 Hz = |240 Hz -f_2|`

`6 Hz = |250 Hz - f_2|`
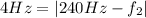
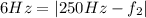
and the solution of this system is
`f_2 = 244 Hz`