Question

Find the positive angle, which satisfies the equation tan^2(x) - tan(x) = 0

I know the answer, but I don't quite understand how to do the question. Please explain how you got the answer if you can.

Answer 1

If it helps, you can replace
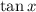
`\tan x` with
`y`. How would you go about solving
`y^2-y=0`?

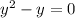
We can write


`\tan x(\tan x-1)=0`

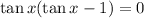
from which we have two possibilities, either
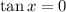
`\tan x=0` or
`\tan x-1=0`.

Both equations have infinitely many solutions because
`\tan x=\tan(x+n\pi)` for any integer
`n`. But we're viewing
`x` as a positive angle, which means
`0<x<2\pi`. Moreover, we can assume
`x` is an acute angle, so that
`0<x<\frac\pi2`.


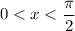
Now,
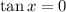
`\tan x=0` for
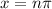
`x=n\pi`, which means there are no solutions to this equation on this interval.


On the other hand,
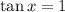
`\tan x=1` for
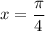
`x=\frac\pi4`.