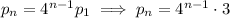Question

1. In an auditorium, there are 21 seats in the first row and 26 seats in the second row. The number of seats in a row continues to increase by 5 with each additional row.

(a) Write an iterative (explicit) rule to model the sequence formed by the number of seats in each row. Show your work.

(b) Use the rule to determine how many seats are in row 15. Show your work.


2. Rhonda started a business. Her business made $40,000 in profits the first year. Her annual profits have increased by an average of 6% each year since then.

(a) Write an iterative rule to model the sequence formed by the profits of Rhonda’s business each year.

(b) Use the rule to determine what the annual profits of Rhonda’s business can be predicted to be 20 years from the start of her business. Round your answer to the nearest dollar. Do not round until the end. Show your work.

3. The sequence 3, 12, 48, 192, … shows the number of pushups Kendall did each week, starting with her first week of exercising.

(a) What is the recursive rule for the sequence?

(b) What is the iterative rule for the sequence?

Answer 1

i will look but i think she was right

Explanation:

Answer 2

1. Let
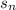
`s_n` be the number of seats in the
`n`-th row. The number seats in the
`n`-th row relative to the number of seats in the
`(n-1)`-th row is given by the recursive rule


`s_n=s_(n-1)+5`


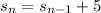
Since
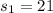
`s_1=21`, we have


`s_2=s_1+5`

`s_3=s_2+5=s_1+2\cdot5`

`s_4=s_3+5=s_1+3\cdot5`

`\cdots`

`s_n=s_(n-1)+5=\cdots=s_1+(n-1)\cdot5`

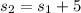
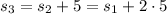
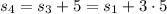
So the explicit rule for the sequence
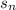
`s_n` is


`s_n=21+5(n-1)\implies s_n=5n+16`

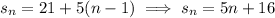
In the 15th row, the number of seats is



`s_(15)=5(15)+16=91`

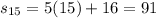
2. Let
`p_n` be the amount of profit in the
`n`-th year. If the profits increase by 6% each year, we would have


`p_2=p_1+0.06p_1=1.06p_1`

`p_3=1.06p_2=1.06^2p_1`

`p_4=1.06p_3=1.06^3p_1`

`\cdots`

`p_n=1.06p_(n-1)=\cdots=1.06^(n-1)p_1`

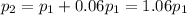
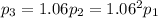
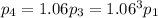
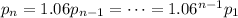
with
`p_1=40,000`.

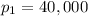
The second part of the question is somewhat vague - are we supposed to find the profits in the 20th year alone? the total profits in the first 20 years? I'll assume the first case, in which we would have a profit of



`p_(20)=1.06^(19)\cdot40,000\approx121,024`

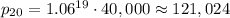
3. Now let
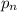
`p_n` denote the number of pushups done in the
`n`-th week. Since
`3\cdot4=12`,
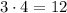
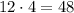
`12\cdot4=48`, and
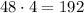
`48\cdot4=192`, it looks like we can expect the number of pushups to quadruple per week. So,


`p_n=4p_(n-1)`

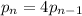
starting with
`p_1=3`.

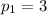
We can apply the same reason as in (2) to find the explicit rule for the sequence, which you'd find to be


`p_n=4^(n-1)p_1\implies p_n=4^(n-1)\cdot3`