Question

The perimeters of similar triangles are in the same ratio as the corresponding sides. Always Sometimes Never

Answer 1

The Perimeter of similar triangles are ALWAYS in same ratio as the corresponding sides.

Explanation:

Triangle is a polygon.

The perimeter of Polygon is sum of all the sides.

⇒Perimeter of Triangle is sum of all three sides.

Let say, we have two similar triangles whose sides are in s :1

Also let sides of a triangle are x, y, & z

then the sides of other triangle are given by : s.x, s.y and s.z

Now, we find the perimeter of triangles

perimeter of first triangle, P = x + x + z

Perimeter of second triangle, P' = s.x + s.y + s.z

⇒ P' = s × (x+ y+ z)

⇒ P' = s × P

⇒
`(P')/(P)=(s)/(1)`

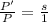
∴ The perimeter of similar triangles are always in the same ratio as the corresponding sides.

Thus, The Perimeter of similar triangles are ALWAYS in same ratio as the corresponding sides.

Answer 2

we know that
the ratio of the perimeters of similar triangles is equal to the scale factor
and
the ratio of the corresponding sides of similar triangles is equal to the scale factor

hence
The perimeters of similar triangles are in the same ratio as the corresponding sides

the answer is
always