Question

What is the average rate of change of the function over the interval x = 0 to x = 4?

f(x)= 2x−1 3x+5 f(x)=2x−13x+5

Enter your answer, as a fraction, in the box.

Answer 1

Applying the formula for the average change of function
`A(x)= (f(x)-f(a))/(x-a)`, we can solve this problem considering that x=4 and a=0. Then, f(4)=2*4-13*4+5=-39 and f(0)=2*0-13*0+5=5, Then
`A(x)= (-39-5)/(4-0) = -9.75`

Answer 2

Average rate of change of function is
`(61)/(400)`.

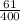Explanation:

Given Function:
`f(x)=(2x-1)/(3x+5)`

To find: Average rate of change of function over interval of x = 0 to x = 4.

We use the the following formula to find the average rate of change of function f(x) over interval x= a and x = b

`Average\:rate\:of\:change\:of\:function=(f(b)-f(a))/(b-a)`

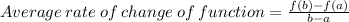
here, a = 0 and b = 4

We find value of f(4) ande f(0)by putting x = 4,

`f(4)=(2*4-1)/(3*4+5)=(8-1)/(12+5)=(7)/(17)=0.41`

`f(0)=(2*0-1)/(3*0+5)=(-1)/(5)=-0.2`

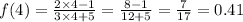
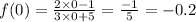
So,

`Average\:rate\:of\:change\:of\:function=(f(4)-f(0))/(4-0)=(0.41-(-0.2))/(4)=(0.41+0.2)/(4)=(0.61)/(4)=(61)/(400)`

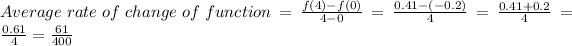
Therefore, Average rate of change of function is
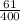`(61)/(400)`.