Answer:
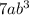 .
.
Explanation:
We have been given three expressions. We are asked to find the greatest common factor of our expressions.
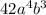 ,
,
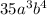 ,
,

The greatest common factor is the factor that divides two or more numbers.
Factors of coefficient:
42: 1, 2, 3, 6,7, 14, 21, 42
35: 1, 5, 7, 35
The greatest common factor of coefficient is 7.
Factors of

Factors of

Factors of
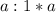
The greatest common factor of
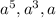 is a.
is a.
Factors of
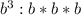
Factors of
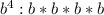
The greatest common factor of
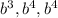 is
is
 .
.
Upon combining all these factors, we will get
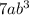 .
.
Therefore, the greatest common factor of
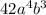 ,
,
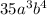 and
and
 is
is
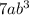 .
.