Question

a 63 kg object needs to be lifted 7 in a matter of 5 Seconds approximately how much horsepowers is required to achieve this task

Answer 1

We need to lift an object from a point A to another point B. So, we have these variables:

For the object:
m = 63Kg

Height:
h = 7in

Time:
t = 5s

Horsepower (hp) is a unit of measurement of power. So, the term was adopted in the late 18th century by Scottish engineer James Watt to compare the output of steam engines with the power of draft horses. So:


`P = (W)/(t)`

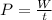
So, we need to calculate the work W. A force is said to do work if, when acting, there is a displacement of the point of application in the direction of the force. In a mathematical language:


`W=Fd`

Given that the displacement is vertically, this force will be:


`F=mg=(63kg)(9.8m/s^(2))=617.4N`

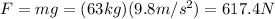
We need to convert the unit in into m, so:

1in = 0.0254m

Then:
7in = 0.1778m

Therefore, as the displacement d = h:


`W = (617.4)(0.1778)=109.77(J)`

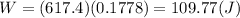
Finally:


`P= (109.77)/(5)=21.95W`

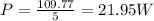
The result is expressed in Watts, so we need to convert it into hp, so:

1hp = 746W


`P= 21.95W((1hp)/(746W))=0.03hp`