Answer: 12
Explanation:
Given : The total number digits given : 4
Since repetition is not allowed then to find the number of different positive integers of 2 digits each can be made with the digits 2, 4, 5, and 8 we use permutations.
We know that the permutation of n things taking m at a time is given by :-
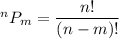
Similarly, the number of permutations of 4 things taking 2 at a time is given by :-
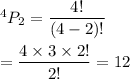
Hence, the required number of different positive integers = 12.