Question

ΔABC and ΔXYZ are similar triangles. If BC = x + 7, AC = x + 6, YZ = 4 − x, and XZ = 3 − x, find the value of x.

A) −
2
3
B) −
3
2
C)
3
2
D)
2
3

Answer 1

I believe the answer is B) -3/2 or -1.5.

Please give a heart and rating if this is right!

Answer 2

Given ΔABC and ΔXYZ are similar triangles. BC = x + 7, AC = x + 6, YZ = 4 − x, and XZ = 3 − x.

Similar triangles have sides in proportion.

`(BC)/(YZ) =(AC)/(XZ)`

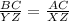
Substituting the given values :

`(x+7)/(4-x) =(x+6)/(3-x)`

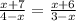
To solve for x we cross multiply

(x+7)(3-x)=(4-x)(x+6)

Using FOIL to multiply

`3x-x^(2) +21-7x =4x+24-x^(2) -6x`

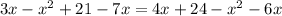
Simplifying like terms

-4x+21=-2x+24

To solve for x we isolate the x term

Adding 2x both sides:

-4x+2x+21=24

-2x+21=24

Subtracting 24 both sides

-2x=24-21

-2x=3

Dividing by -2 we have x=
`-(3)/(2)`

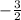
Option B is the right answer.