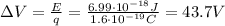The De Broglie wavelength of the electron is equal to
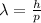
where h is the Planck constant and p is the electron's momentum. Since this wavelength must be equal to that of the x-ray,
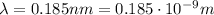
we can re-arrange the previous equation to find the momentum of the electron:
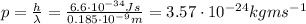
The kinetic energy of the electron is equal to the square of the momentum divided by twice its mass:
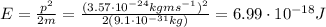
When the electron is accelerated by a potential difference
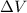 , the energy it gains is
, the energy it gains is
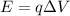
where q is the electron charge. Re-arranging the formula, we find the potential difference: