Question

Star a has an absolute magnitude of 8. what is its apparent magnitude at a distance of 100 pc

Answer 1

From the definition of apparent magnitude, we know that:

`m_(1) - m_(2) = -2.5Log( (F_(1))/(F_(2)) )`
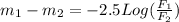
where:
m = apparent magnitude
F = corresponding flux

We also know that the flux is given by the formula:

`F = (L)/(4 \pi d^(2) )`
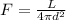
where:
L = luminosity
d = distance

Therefore:

`(F_(1) )/(F_(2)) = ((L_(1) )/(4 \pi d_(1)^(2) ))((4 \pi d_(2)^(2) )/(L_(2) )) \\ = (L_(1)d_(2)^(2))/(L_(2)d_(1)^(2))`

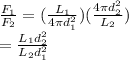
Now, let's apply these formulae to the same star (therefore, same luminosity), using apparent magnitude and absolute magnitude (which is defined as the apparent magnitude the star would have if it were at a distance of 10pc):

`m - M = 2.5 Log ( (d)/(10pc))^(2)`

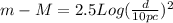
Now, let's solve for m:

`m = M + 2.5 Log ( (d)/(10))^(2)`
=
`8 + 2.5 Log ( (100)/(10))^(2)`
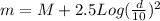
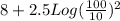
= 13

Hence, the apparent magnitude of the star would be m = +13