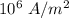Question

A hollow copper wire with an inner diameter of 0.50 mm and an outer diameter of 1.8 mm carries a current of 15

a. what is the current density in the wire?

Answer 1

The current density in the hollow copper wire is
`2.59` ×
`10^(6) \;A/m^2`

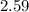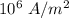
Given the following data:

• Inner diameter of wire = 0.50 mm

• Outer diameter of wire = 1.8 mm

• Current = 15 Amps.

To find the current density in the hollow copper wire:

First of all, we would determine the radius and the cross-sectional area of the hollow copper wire.

`Inner \; radius = (Inner\;diameter)/(2) \\\\Inner \; radius = (0.5)/(2)`

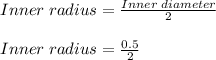
Inner radius = 0.25 mm

`Outer \; radius = (Outer\;diameter)/(2) \\\\Outer \; radius = (1.8)/(2)`

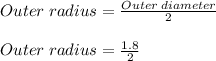
Outer radius = 0.9 mm

Next, we would determine its cross-sectional area:

`A = \pi (O^2 - I^2)`

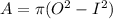
Where:

• O is the outer radius of the wire.

• I is the inner radius of the wire.

• A is the cross-sectional area.

Substituting the given parameters into the formula, we have;

`A = \pi (0.9^2 - 0.25^2)\\\\A = \pi (0.81 - 0.625)\\\\A = 3.142(0.185)`

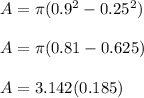
A = 0.58
`mm^2`

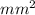
In square meters;

Area =
`0.58` ×
`10^(-6) \;m^2`

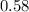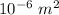
Mathematically, current density is given by the formula:

`J = (I)/(A)\\\\J = (15)/(0.58(10^(-6)))`

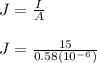
Current density, J =
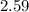`2.59` ×
`10^(6) \;A/m^2`

Answer 2

The current density is equal to the current intensity divided by the cross-sectional area through which the current passes:

`J= (I)/(A)`

The inner radius of the wire is

`r_i = (0.50 mm)/(2)=0.25 mm`
while the outer radius is

`r_o = (1.80 mm)/(2)=0.90 mm`
Therefore the cross-sectional area of the wire is

`A= \pi (r_o^2 - r_i^2)=\pi ((0.9mm)^2-(0.25 mm)^2)=2.35 mm^2`

`= 2.35 \cdot 10^(-6) m^2`

So the current density in the wire is

`J= (I)/(A)= (15 A)/(2.35 \cdot 10^(-6) m^2)=6.38 \cdot 10^6 A/m^2`