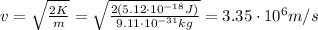The force experienced by the electron due to the electric field is given by:

The work done by the field over a distance of d=4 cm=0.04 m is equal to the energy acquired by the electron during its motion:
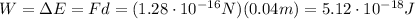
Since the electron starts from rest, its initial kinetic energy is zero, so this energy acquired is equal to the final kinetic energy of the electron:
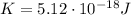
And from the formula

we can find the speed of the electron: