Question

The graph of the continuous function g, the derivative of the function f, is shown above. The function g is piecewise linear for -5 ≤ x < 3 and g(x) = 2(x-4)^2 for 3 ≤ x ≤ 6.

(a) If f(1) = 3, what is the value of f(-5) ?

(b) Evaluate \int_{0}^{6} g(x)\; dx .

(c) For -5 < x < 6, on what open intervals, if any, is the graph of f both increasing and concave up? Give a reason for your answer.

(d) Find the x-coordinate of each point of inflection of the graph of f. Give a reason for your answer.

(This was on the no-calculator section of the recently-released AP Calculus AB 2018 exam so I appreciate it if you tried to limit calculator usage)

Answer 1

a) We know that g is the derivative of f, therefore to find f(x), we find the anti-derivative of g(x). This is just the area under the curve.

We are given f(1) = 3, so to find f(-5) we need to find the area under the curve from x = -5 to x = 1 then subtract it from f(1).

The area from x=-5 to x=-1 is -10.5

The area from x=0 to x=1 is 1.

So f(-5) = 3 - (-10.5+1) = 12.5

b) In this part, we are doing basically the same thing, but we don't need to deal with an initial value.

The area under the curve from x=1 to x=3 is 4.

To find the area under the curve from x=3 to x=6, we need to integrate 2(x-4)^2


`\int\limits^6_3 {2(x-4)^2} \, dx`


`\int\limits^6_3 {2(x^2-8x+16)} \, dx`


`\int\limits^6_3 {(2x^2-16x+32)} \, dx`

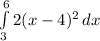
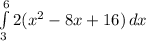
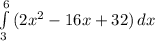
If you need help integrating this, let me know. Otherwise the answer is 6.

Add the integral from (1,3) to the integral from (3,6) to get the answer to part b.

The answer is 10.

c) The graph is increasing when g > 0, and it is concave up when g' > 0. This means we are looking for sections of the graph of g that are above the x-axis and increasing.

The answer is (0,3)∪(4,6)

Note: I don't know how the College Board would rule this one. They may say it's (0,1)∪(4,6) because the graph of f on the interval (1,3) is linear. Therefore it is technically concave up AND down. Might want to ask your teacher about this.

d) The points of inflection are the minima and maxima of g (where g changes from increasing to decreasing or vice versa).

The graph of f has points of inflection at x=3 and x=4 because g changes from increasing to decreasing at x = 3, and g changes from decreasing to increasing at x = 4.

Note: Again, we run into the issue where g is flat on the interval (1,3). I've never come across a scenario like this where there appears to be a "region" of inflection rather than a point, so I would say the point of inflection is at x=3.

Answer 2

(a)

f is the antiderivative of g


`\int_(-5)^1g(x)\,dx=f(1)-f(-5) \implies f(-5) = f(1) - \int_(-5)^1 g(x)\, dx`

We calculate
`\int_(-5)^1 g(x)\, dx` using geometry.

For x ∈ [-5,-1], g is a negative trapezoid. If the area of a trapezoid is 1/2(a+b)(h), then a = 4, b = 3, h = -3. The area here is therefore


`\int_(-5)^(-1) g(x)\, dx = (1)/(2)(4+3)(-3) = -21/2`

For x ∈ [-1,0], g has no area between the curve and the x-axis. Therefore,
`\int_(-1)^0 g(x)\, dx = 0`

For x ∈ [0,1], g is a positive triangle. If the area of a triangle is 1/2bh, then b = 1 and h = +2. The area here is therefore


`\int_(0)^1 g(x)\, dx = (1)/(2)(1)(2) = 1`

Thus


`\int_(-5)^1 g(x)\, dx = -(21)/(2) + 0 + 1 = -19/2`

Hence


`f(-5) = f(1) - \int_(-5)^1 g(x)\, dx \implies f(5) = 3 - \left(-(19)/(2)\right) \implies\\ \\ f(5) = 25/2`

_____________

(b)

For
`\int_1^6g(x)\, dx =\int_0^3g(x)\, dx + \int_3^6g(x)\, dx`


`\int_1^6g(x)\, dx = b h = (2)(2) = 4`


`\int_3^6g(x)\, dx = \int_3^6 2(x-4)^2\, dx = 2\int_3^6 (x-4)^2 \implies \\ \\ u = x - 4 \colon {{u(6) = 2} \atop {u(3) = -1}} \text{ (Changing limits of integration)}\\ \\ \implies 2\int_(-1)^(2) u^2 du = 2 \left[ (u^3)/(3) \right]_(-1)^(2) \\ \implies 2\left( (2^3)/(3) - ((-1)^3)/(3) \right) \\ \implies 6`

Thus


`\int_1^6g(x)\, dx =4 + 6 = 10`

_____________

(c)

The graph of f is both increasing and concave up on the intervals 0 < x < 1 and 4 < x < 6 because the derivative of f, which is the function g graphed above, is positive and increasing.

_____________

(d)

The graph of f has an inflection point at x = 4 because the derivative of f changes from decreasing to increasing at this point.