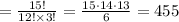Question

How many ways can 12 passengers be seated in a small airplane with 15 seats

Answer 1

455

Explanation:

This is a combinatorics problem.

It is asking us the number of ways a sample of r elements can be obtained from a larger set of n objects where order does not matter and repetitions are not allowed

It is called n choose k and the formula is

`C(n,r) = \binom{n}{r} = (n!)/(( r! (n - r)! ))`

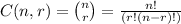
Here the ! symbol represents the factorial of that number

For example,

`n! = n\cdot(n-1)\cdot(n-2)......\cdot3\cdot2\cdot 1`

Here n = 15 and r = 12

How many ways can we arrange 12 people in 15 slots

`C(n,r) = C(15,12)`

`= (15!)/(( 12! (15 - 12)! ))`

`= (15!)/(12! * 3! )`

`= 455`

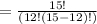
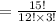
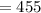
You can use a calculator to do this but noting that

15! = 15 x 14 x 13 x 12! and 3! = 3 x 2 = 6 we get

`= (15!)/(12! * 3! ) = (15\cdot14\cdot13)/(6) = 455`