Question

The graph of the continuous function g, the derivative of the function f, is shown above. The function g is piecewise linear for -5 ≤ x < 3 and g(x) = 2(x-4)^2 for 3 ≤ x ≤ 6.

(a) If f(1) = 3, what is the value of f(-5) ?

(b) Evaluate
`\int_(0)^(6) g(x)\; dx` .

(c) For -5 < x < 6, on what open intervals, if any, is the graph of f both increasing and concave up? Give a reason for your answer.

(d) Find the x-coordinate of each point of inflection of the graph of f. Give a reason for your answer.

(This was on the no-calculator section of the recently-released AP Calculus AB 2018 exam so I appreciate it if you tried to limit calculator usage)

Answer 1

a)
`g=f'` is continuous, so
`f` is also continuous. This means if we were to integrate
`g`, the same constant of integration would apply across its entire domain. Over
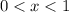
`0<x<1`, we have
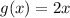
`g(x)=2x`. This means that



`f_(0<x<1)(x)=\displaystyle\int2x\,\mathrm dx=x^2+C`


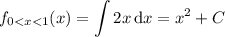
For
`f` to be continuous, we need the limit as
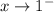
`x\to1^-` to match
`f(1)=3`. This means we must have



`\displaystyle\lim_(x\to1)x^2+C=1+C=3\implies C=2`


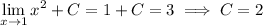
Now, over
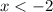
`x<-2`, we have
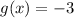
`g(x)=-3`, so
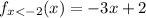
`f_(x<-2)(x)=-3x+2`, which means
`f(-5)=17`.


b) Integrating over [1, 3] is easy; it's just the area of a 2x2 square. So,



`\displaystyle\int_1^6g(x)=4+\int_3^62(x-4)^2\,\mathrm dx=4+6=10`


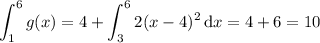
c)
`f` is increasing when
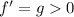
`f'=g>0`, and concave upward when
`f''=g'>0`, i.e. when
`g` is also increasing.

We have
`g>0` over the intervals
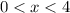
`0<x<4` and
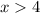
`x>4`. We can additionally see that
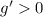
`g'>0` only on
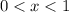
`0<x<1` and
`x>4`.


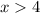
d) Inflection points occur when
`f''=g'=0`, and at such a point, to either side the sign of the second derivative
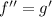
`f''=g'` changes. We see this happening at
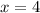
`x=4`, for which
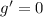
`g'=0`, and to the left of
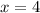
`x=4` we have
`g` decreasing, then increasing along the other side.


We also have
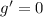
`g'=0` along the interval
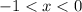
`-1<x<0`, but even if we were to allow an entire interval as a "site of inflection", we can see that
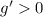
`g'>0` to either side, so concavity would not change.