Question

Billy is analyzing a circle, y2 + x2 = 81, and a linear function g(x). Will they intersect? y2 + x2 = 81 g(x) graph of the function y squared plus x squared equals 81 x g(x) −1 −8.5 0 −9 1 −9.5

Answer 1

YES, they will intersect.

Explanation:

The equation of circle with center at origin i.e. (0,0) and radius 9 is given by:

`x^2+y^2=81`

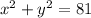
Also, we are given a linear function g(x) whose set of values in table is given by:

x g(x)

−1 −8.5

0 −9

1 −9.5

Now, we find the equation of line with the help of two points.

We know that the equation of a line passing through (a,b) and (c,d) is given by:

`y-b=(d-b)/(c-a)* (x-a)`

We have:

(a,b)=(-1,-8.5) and (c,d)=(0,-9)

Hence, the equation of g(x) is:

`g(x)-(-8.5)=(-9-(-8.5))/(0-(-1))* (x-(-1))\\\\g(x)+8.5=(-0.5)/(1)* (x+1)\\\\g(x)=-0.5x-0.5-8.5\\\\g(x)=-0.5x-9`

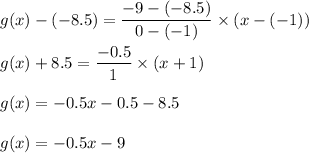
Hence,

g(x)= -0.5x-9

Now we plot the graph of circle and the linear function g(x) and see whether they will intersect or not.

Yes, the graph of the two functions will intersect.

The point of intersection are:

(-7.2,-5.4) and (0,-9)

Answer 2

we have that
x²+y²=81

x g(x)
-1 -8.5
0 -9.1
1 -9.5

using a graph tool
see the attached figure

the answer is
both graphs intersect at two points